A Fundamental Principle in Atomic and Molecular Structure

Maria
Chemistry
02 Sep, 2024

Hund's Rule, named after the German physicist Friedrich Hund, is a principle in quantum mechanics that explains how electrons are distributed in atomic orbitals of the same energy (degenerate orbitals) to minimize repulsion and achieve the most stable electron configuration. Hund’s Rule plays a crucial role in understanding the electronic structure of atoms and molecules, and by extension, the chemical properties of elements.

In this article, we will explore Hund's Rule in detail, its significance in electron configuration, and its implications in various fields of chemistry and physics.

Hund's Rule states:

For orbitals of equal energy (degenerate orbitals), electrons will fill each orbital singly before pairing up in any orbital. Furthermore, all unpaired electrons in singly occupied orbitals will have the same spin.

Key Aspects of Hund's Rule

Singly Occupied Orbitals First: When electrons are added to degenerate orbitals (orbitals of the same energy, such as the three p orbitals or five d orbitals), they will first occupy each orbital singly before any orbital receives a second electron. This minimizes electron-electron repulsion within an atom or molecule.
Parallel Spins: Electrons occupying these singly filled orbitals will have the same spin (either all spin-up or all spin-down). This alignment of spins helps to further reduce repulsion between electrons, leading to a more stable configuration.

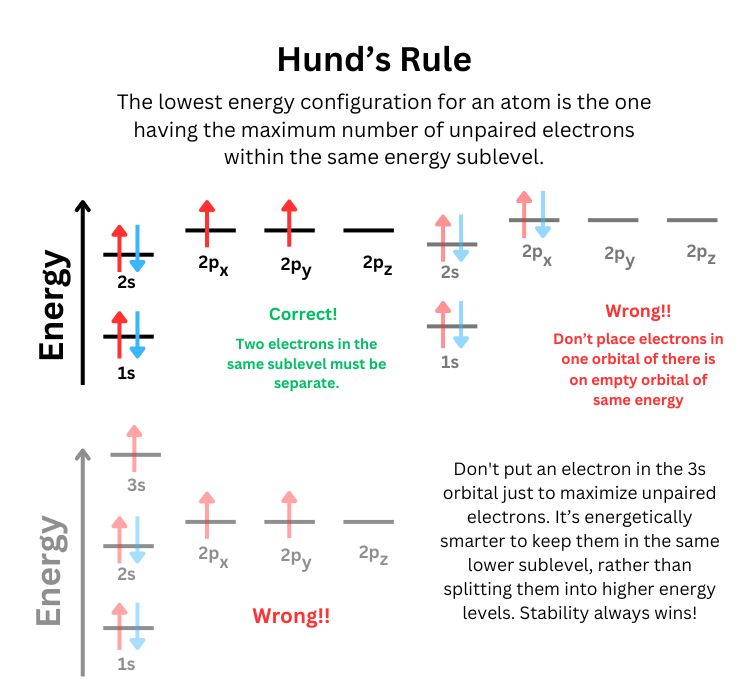
Illustration with Examples

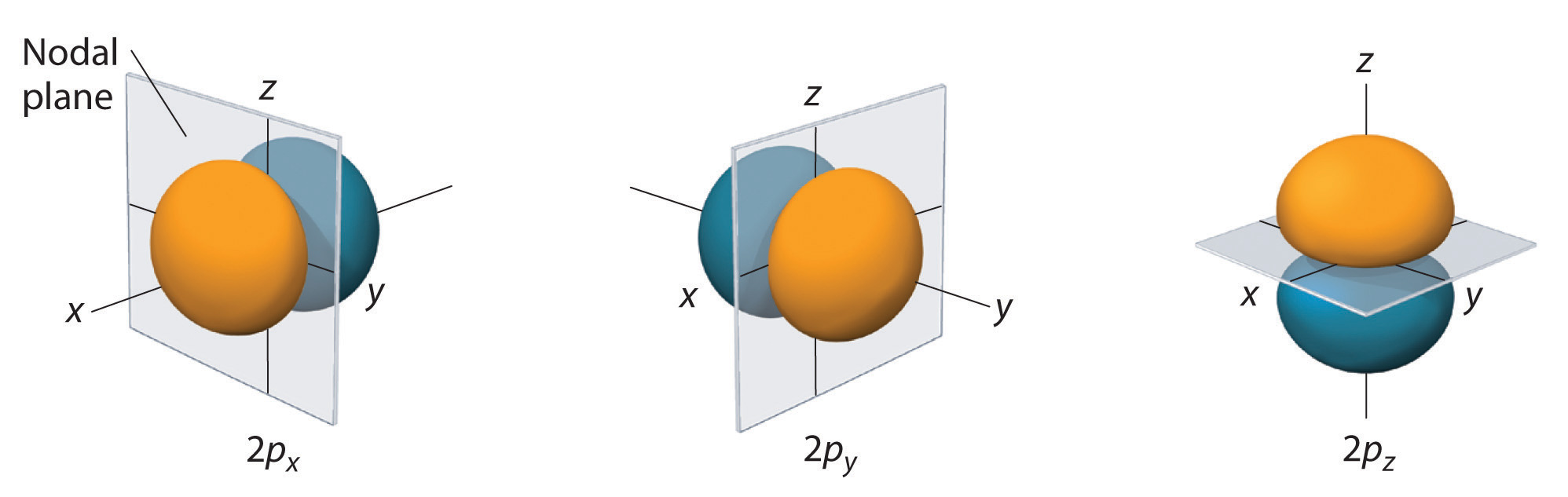
p Orbitals: For a p subshell (which consists of three degenerate p orbitals), if there are three electrons, they will each occupy a different p orbital (e.g., 2p_x^1, 2p_y^1, and 2p_z^1), all with the same spin before any of them pairs up.
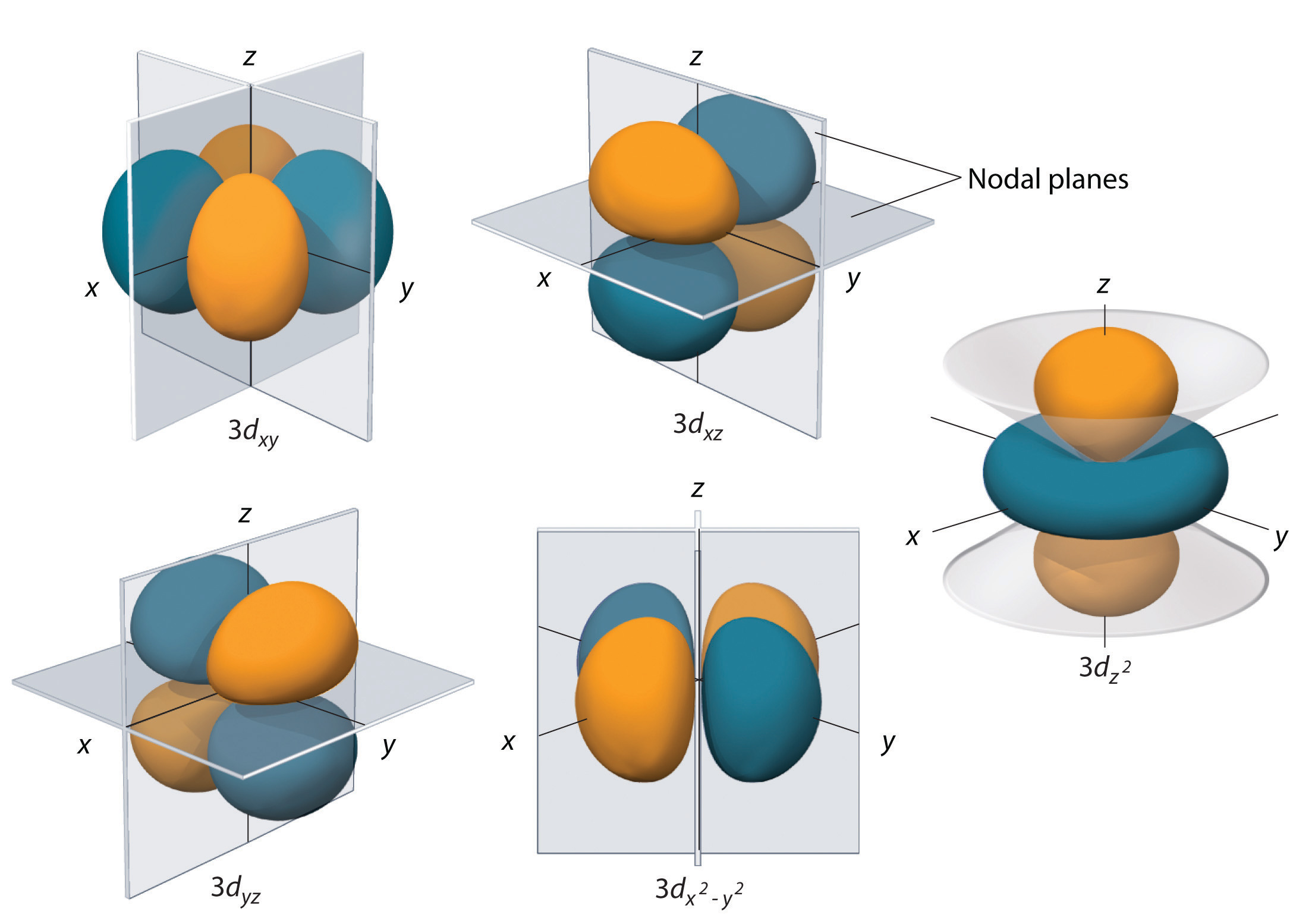
d Orbitals: For a d subshell (which consists of five degenerate d orbitals), if there are five electrons, they will each occupy a different d orbital (e.g., 3d*(xy)^1, 3d*(xz)^1, 3d*(yz)^1 , 3d_z²^1, 3d*(x²-y²)^1), all with the same spin before pairing occurs.

Hund's Rule helps to explain the observed electron configurations of atoms and the stability of different electron arrangements by minimizing repulsion and maximizing exchange energy.

Explanation of Hund’s Rule Using Quantum Numbers

To understand Hund's Rule, we need to review the quantum numbers that describe the arrangement of electrons in atoms:

Principal Quantum Number (n): Specifies the energy level or shell.
Azimuthal Quantum Number (l): Describes the subshell or shape of the orbital (s, p, d, f).
Magnetic Quantum Number (m_l): Describes the orientation of the orbital in space.
Spin Quantum Number (m_s): Specifies the electron's spin, which can either be +1/2 (spin-up) or -1/2 (spin-down).

In a given subshell (e.g., the p, d, or f subshell), there are multiple orbitals that have the same energy. These orbitals are called degenerate orbitals. Hund's Rule governs how electrons are placed in these degenerate orbitals by stating that electrons will fill each orbital singly, with spins aligned, before any electrons are paired in the same orbital.

Why Does Hund's Rule Minimize Energy?

Hund's Rule is based on the principle of minimizing electron-electron repulsion within an atom. Electrons, being negatively charged particles, naturally repel each other. By occupying different orbitals singly rather than pairing up in the same orbital, electrons stay as far apart as possible, which reduces the electrostatic repulsion between them. Additionally, having the same spin creates a quantum mechanical effect called exchange energy, which further stabilizes the atom.

When electrons have the same spin (parallel spins), there is a reduction in their coulombic repulsion, leading to a more stable, lower-energy configuration. In contrast, placing two electrons in the same orbital (with opposite spins, as required by the Pauli Exclusion Principle) increases repulsion and raises the overall energy of the system.

Application of Hund's Rule in Atomic Orbitals

Hund's Rule is a fundamental principle in quantum chemistry that governs the distribution of electrons in atomic orbitals of equal energy. This rule is crucial for understanding the electron configurations of atoms and has significant implications for chemical bonding, magnetic properties, and periodic trends. Here’s a detailed exploration of how Hund’s Rule applies to atomic orbitals.

Hund’s Rule in the p Orbitals

The p orbitals are a set of three degenerate orbitals (i.e., they have the same energy) within the same principal energy level. These orbitals are labeled p_x , p_y, and p_z .

Single Occupancy: According to Hund’s Rule, when filling the p orbitals, electrons will first occupy each of the three orbitals singly before any of the orbitals receive a second electron. This minimizes electron-electron repulsion within the orbitals.
Spin Alignment: Electrons in singly occupied p orbitals will have parallel spins (all spin-up or all spin-down), which further stabilizes the atom by reducing repulsion.

Example:

Carbon (atomic number 6): The electron configuration is 1s² 2s² 2p². The two electrons in the 2p orbitals will occupy two of the three degenerate p orbitals singly (e.g., 2p_x² and 2p_y² ), with parallel spins.

Hund’s Rule in the d Orbitals

The d orbitals are a set of five degenerate orbitals within a given principal energy level. These orbitals are labeled d*(xy) , d*(xz) , d*(yz), d_z², and d*(x² - y²) .

Single Occupancy: When filling the d orbitals, electrons will first occupy each of the five orbitals singly before pairing begins. This arrangement minimizes repulsion among electrons and stabilizes the atom.
Spin Alignment: Electrons in singly occupied d orbitals will have parallel spins.

Example:

Chromium (atomic number 24): The electron configuration is [Ar] 4s^1 3d^5 . Rather than following the expected [Ar] 4s^2 3d^4 configuration, one electron from the 4s orbital is promoted to the 3d orbitals. This results in a half-filled d subshell, which is more stable due to the arrangement of electrons in separate d orbitals with parallel spins.

Hund’s Rule in the f Orbitals

The f orbitals are a set of seven degenerate orbitals within a given principal energy level. These orbitals are more complex in shape and have more sub-levels.

Single Occupancy: Electrons will fill the seven f orbitals singly before any orbital receives a second electron. This pattern reduces repulsion and leads to greater stability.
Spin Alignment: Electrons in singly occupied f orbitals will have parallel spins.

Example:

Neodymium (atomic number 60): The electron configuration is [Xe] 4f^4 6s^2 . The four electrons in the 4f orbitals will occupy four of the seven degenerate f orbitals singly (e.g., 4f*1^1, 4f*2^1, 4f*3^1, 4f*4^1 ), with parallel spins.

Implications of Hund’s Rule for Magnetic Properties

Hund’s Rule directly influences the magnetic properties of atoms and ions. The presence of unpaired electrons (due to Hund’s Rule) leads to paramagnetism, where the atom or ion is attracted to external magnetic fields. Atoms with unpaired electrons exhibit stronger magnetic interactions.

Example: Oxygen (atomic number 8) has two unpaired electrons in the 2p orbitals, resulting in its paramagnetic behavior. This property can be observed experimentally using techniques like electron paramagnetic resonance (EPR).

Hund’s Rule and Chemical Bonding

Hund’s Rule also affects the formation of chemical bonds and the overall stability of molecules. In molecular orbital theory, it helps explain how electrons fill degenerate molecular orbitals:

In molecular oxygen (O₂), for instance, the electrons fill the degenerate π* orbitals according to Hund’s Rule, leading to a stable arrangement that contributes to the molecule’s paramagnetic nature.

Hund’s Rule and the Periodic Table

Hund's Rule helps explain the chemical behavior of elements, especially within a group or period in the periodic table. The way electrons are arranged in degenerate orbitals affects the magnetic properties of elements and their chemical reactivity:

Paramagnetism: Atoms or ions with unpaired electrons (due to Hund's Rule) exhibit paramagnetism—they are attracted to external magnetic fields. For example, oxygen is paramagnetic because of its unpaired electrons in the π* orbitals.
Chemical Properties: Elements with similar electron configurations, especially those governed by Hund's Rule, tend to exhibit similar chemical properties. For example, nitrogen (atomic number 7) and phosphorus (atomic number 15), both having three unpaired p-electrons, share similar bonding characteristics.

Hund’s Rule and Exchange Energy

The principle of maximizing the number of unpaired electrons with parallel spins introduces the concept of exchange energy. Exchange energy is the additional stabilization that arises when electrons with parallel spins can exchange places in degenerate orbitals. This exchange reduces the probability of finding two electrons in close proximity, thus lowering the system’s overall energy.

The greater the number of parallel spins, the greater the exchange energy and the more stable the atom or molecule becomes. This is why half-filled and fully filled subshells are often more stable than partially filled subshells with paired electrons, as the configuration minimizes repulsion and maximizes exchange energy.

Violations and Limitations of Hund’s Rule

While Hund’s Rule applies to most cases, there are situations where it appears to be violated. These usually involve:

Complex ions: In coordination chemistry, ligands surrounding a metal ion can influence orbital energies, sometimes leading to paired electrons in lower-energy orbitals even before higher-energy orbitals are singly occupied. This is especially true in cases of strong field ligands, where the energy gap between orbitals is significant.
Excited states: In excited states of atoms, electrons can be promoted to higher orbitals, temporarily violating Hund’s Rule.

However, these violations are exceptions rather than the rule and occur under specific circumstances where other forces, such as ligand interactions or external energy input, become significant.

Chemistry FAQ

Hund's Rule is connected to exchange energy, a quantum mechanical effect that arises when electrons with parallel spins can "exchange" positions within degenerate orbitals. This exchange interaction results in a lower energy state for the atom. The more unpaired electrons there are with the same spin, the more possible exchanges, and thus, the greater the exchange energy. This additional stability is a key reason why atoms prefer configurations with maximum unpaired electrons and aligned spins.

In simple terms, Hund's Rule maximizes exchange energy, reducing electron-electron repulsion and leading to a more stable atomic or molecular configuration.

In certain transition metals and lanthanides, Hund's Rule may appear to be violated due to the very close energy levels of different orbitals (e.g., d and s orbitals in transition metals). In cases where the stability gained by half-filled or fully filled d-orbitals outweighs the stability predicted by Hund's Rule, exceptions arise.

For instance, chromium (Cr) and copper (Cu) exhibit anomalous electron configurations ([Ar] 3d⁵ 4s¹ and [Ar] 3d¹⁰ 4s¹, respectively) because a half-filled or fully filled d-subshell provides extra stability, even if it requires the 4s orbital to be partially filled.

These exceptions reflect the complex interplay between Hund's Rule, orbital energy levels, and other factors such as shielding and subshell stability.

Paramagnetism arises in atoms or molecules with unpaired electrons, as Hund’s Rule dictates that degenerate orbitals should be singly occupied with parallel spins before pairing occurs. The unpaired electrons have magnetic moments that cause the atom or molecule to be attracted to an external magnetic field.

A classic example is molecular oxygen (O₂), which has two unpaired electrons in its π* orbitals, resulting in its paramagnetic behavior. The application of Hund's Rule explains why these electrons remain unpaired, as pairing them would require occupying the same orbital, leading to higher repulsion and a less stable configuration.

Hund’s Rule extends beyond atomic orbitals to molecular orbitals as well. In molecules like O₂, degenerate π orbitals are filled according to Hund's Rule. This results in two unpaired electrons occupying two degenerate π* (antibonding) orbitals, each with parallel spins.

The unpaired electrons explain oxygen’s paramagnetic nature, which cannot be explained by a simple Lewis structure. Hund’s Rule ensures that these electrons do not pair up until each degenerate orbital is singly occupied, even in molecular orbitals.

In complex molecules, the rule applies similarly to degenerate bonding or antibonding orbitals, dictating how electrons are distributed and influencing the molecule's magnetic and chemical properties.

Hund's Rule often leads to extra stability in half-filled and fully filled subshells. This is particularly true for the p, d, and f subshells. A half-filled subshell (e.g., d⁵) has electrons occupying each orbital singly with parallel spins, which maximizes exchange energy and minimizes repulsion. Similarly, a fully filled subshell (e.g., d¹⁰) provides even more stability due to the symmetrical electron distribution and minimized energy interactions.

The stability of half-filled (e.g., Mn with 3d⁵) and fully filled (e.g., Zn with 3d¹⁰) subshells can explain various chemical properties, including ionization energies, oxidation states, and the formation of stable complexes in these elements. This rule is pivotal in predicting and understanding the electron configurations of elements, especially in transition metals and their compounds.

Conclusion

Hund's Rule is an essential concept for understanding the arrangement of electrons in atoms and molecules, especially in orbitals of the same energy. It helps explain how electrons minimize repulsion by occupying degenerate orbitals singly and with parallel spins, providing a stable, low-energy configuration for atoms and molecules. Hund’s Rule is fundamental to predicting the magnetic properties, chemical reactivity, and overall stability of elements and compounds across the periodic table.

By ensuring that unpaired electrons are maximized and have the same spin, Hund’s Rule is key to the intricate dance of electrons that defines the structure of matter in the quantum world.

Tags :