Understanding the Pauli Exclusion Principle: A Cornerstone of Quantum Mechanics

Maria
Chemistry
29 Aug, 2024

The Pauli Exclusion Principle is one of the most fundamental concepts in quantum mechanics and plays a crucial role in explaining the behavior of particles in atoms, molecules, and solids. Proposed by Austrian physicist Wolfgang Pauli in 1925, the principle is essential for understanding why matter has the structure it does, why elements in the periodic table behave differently, and why matter occupies space rather than collapsing into a singularity. This article delves into the details of the Pauli Exclusion Principle, its implications, and its significance in modern physics.

The Basic Statement of the Pauli Exclusion Principle

The Pauli Exclusion Principle is a fundamental concept in quantum mechanics that states:

No two fermions can occupy the same quantum state within a quantum system simultaneously.

In more detail, this principle asserts that:

Unique Quantum States for Fermions: Within a given quantum system (such as an atom), no two identical fermions (particles with half-integer spin, such as electrons, protons, and neutrons) can have the same set of quantum numbers. Each fermion must occupy a unique quantum state.
Quantum Numbers and the Exclusion Principle: The quantum state of a particle is described by a set of four quantum numbers:
- Principal Quantum Number (n): Indicates the energy level or shell.
- Azimuthal Quantum Number (l): Specifies the shape of the orbital (s, p, d, f).
- Magnetic Quantum Number (m_l): Describes the orientation of the orbital in space.
- Spin Quantum Number (m_s): Represents the intrinsic spin of the particle, which can be +1/2 or -1/2 According to the Pauli Exclusion Principle, no two fermions in the same system can have the same set of all four quantum numbers.
Application to Electrons in Atoms: In atoms, this principle explains the arrangement of electrons in atomic orbitals. For example:
- Each orbital in an atom can hold a maximum of two electrons, with opposite spins. This is because the Pauli Exclusion Principle requires that no two electrons in an atom can have identical quantum numbers. Therefore, the two electrons in a given orbital must have different spin quantum numbers to satisfy the principle.
Significance in Quantum Mechanics: The Pauli Exclusion Principle is crucial for the stability and structure of matter. It accounts for the electron configuration of atoms, the structure of the periodic table, and the properties of materials. Without this principle, matter would not have the same structure or stability, and phenomena such as the electron shell structure and chemical bonding would be vastly different.

Quantum Numbers and Electron Configuration

To fully grasp the Pauli Exclusion Principle, it's essential to understand the four quantum numbers that define the state of an electron in an atom. These quantum numbers help describe the "address" of each electron in an atom:

Principal Quantum Number (n):
- This number describes the energy level or shell in which the electron resides. The value of n is a positive integer (1, 2, 3,...).
Azimuthal Quantum Number (l):
- Also known as the angular momentum quantum number, l describes the shape of the electron’s orbital (spherical, dumbbell-shaped, etc.). It can take values from 0 to (n - 1).
Magnetic Quantum Number (m_l):
- The magnetic quantum number describes the orientation of the electron's orbital in space and can take integer values between -l and +l, including 0.
Spin Quantum Number (m_s):
- This number describes the spin of the electron, which can be either +1/2 or -1/2. This intrinsic property of electrons creates two possible orientations for each electron in a given orbital.

For example, in the case of an electron in the first energy level (n = 1), the possible quantum numbers are:

n = 1, l = 0, m_l = 0, and m_s can be either +1/2 or -1/2.

According to the Pauli Exclusion Principle, no two electrons in the same atom can have an identical set of these four quantum numbers. This restriction fundamentally explains the structure of electron shells and subshells in atoms.

The Principle in Atomic Structure

In atoms, the Pauli Exclusion Principle is the reason for the arrangement of electrons into shells and subshells. It explains why each orbital can hold a maximum of two electrons, each with opposite spins. For example:

The 1s orbital (n = 1, l = 0, m_l = 0) can accommodate two electrons, but they must have opposite spins (one with m_s = +1/2 and the other with m_s = -1/2).
If one of these quantum numbers were the same for both electrons, it would violate the Pauli Exclusion Principle.

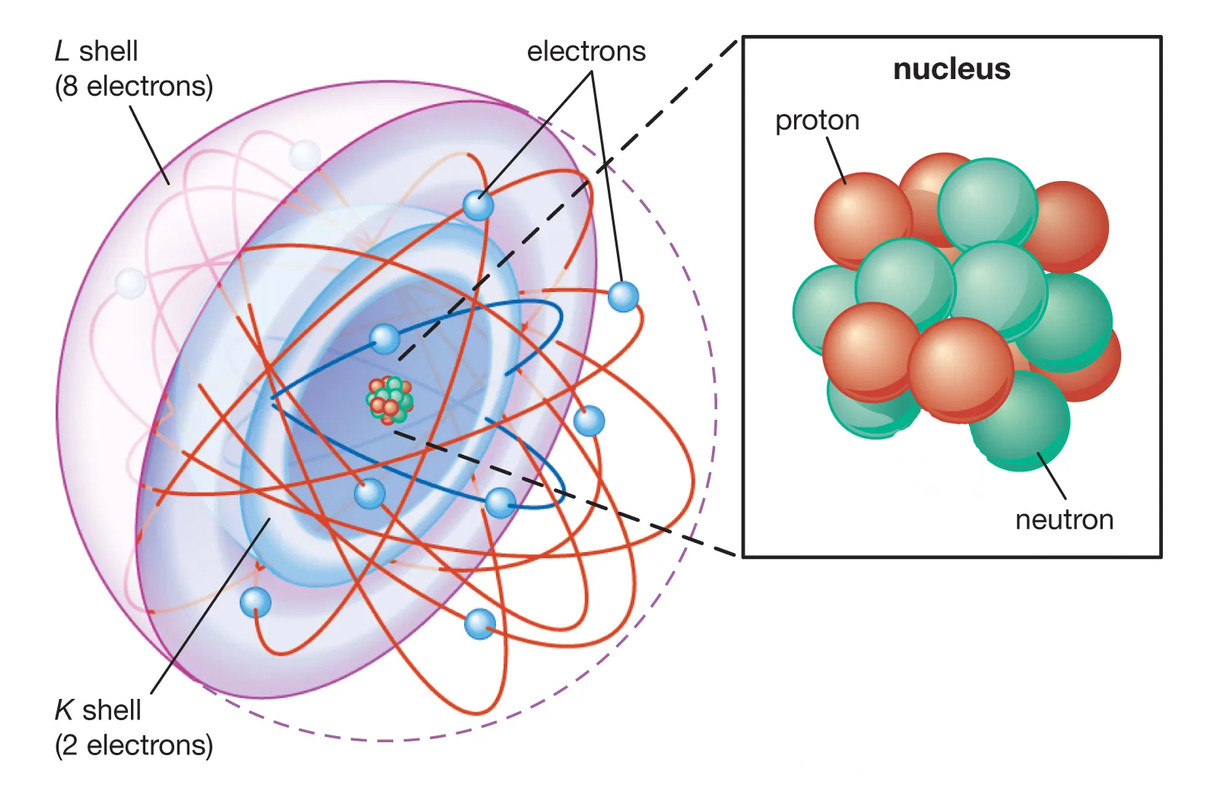
Atomic Structure

This principle is why electrons fill available orbitals in such a way that no two electrons in a given atom have the same set of quantum numbers. For instance, the periodic table’s structure, with its division into periods and groups, directly results from the Pauli Exclusion Principle. It explains why elements like helium (atomic number 2) have fully filled 1s orbitals, and why elements like neon (atomic number 10) fill the 2s and 2p orbitals before beginning to occupy the next shell.

This principle is crucial for understanding atomic structure, electron configuration, and the behavior of electrons in atoms and molecules. Here’s an in-depth look at how the Pauli Exclusion Principle applies to atomic structure:

Quantum Numbers

To grasp the Pauli Exclusion Principle, it's essential to understand the four quantum numbers that describe an electron's state in an atom:

Principal Quantum Number (n): Indicates the main energy level or shell of the electron. Values are positive integers (1, 2, 3, ...).
Azimuthal Quantum Number (l): Defines the shape of the orbital and is related to the subshell (s, p, d, f). Values range from 0 to ( n-1 ).
Magnetic Quantum Number (m_l): Specifies the orientation of the orbital in space. It ranges from -l to +l.
Spin Quantum Number (m_s): Describes the intrinsic spin of the electron. It can be either +1/2 (spin-up) or -1/2 (spin-down).

The Principle's Implications for Electron Configuration

Unique Quantum State

The Pauli Exclusion Principle implies that each electron in an atom must have a unique set of quantum numbers. This uniqueness means:

No two electrons in an atom can share the same values for n , l, m_l, and m_s simultaneously.
As a result, an orbital can hold a maximum of two electrons, each with opposite spins (one with m_s = +1/2 and one with m_s = -1/2 ).

Example: Helium Atom

In a helium atom, the electron configuration is 1s^2 .
The 1s orbital, having n = 1 and l = 0 , can accommodate two electrons. These two electrons have opposite spins to satisfy the Pauli Exclusion Principle.

Example: Oxygen Atom

The electron configuration of oxygen is 1s^2 2s^2 2p^4 .
The 2p subshell has three degenerate orbitals ( 2p_x, 2p_y ,2p_z ). Each of these orbitals can hold up to two electrons with opposite spins.
In oxygen, the 2p subshell contains four electrons. According to the Pauli Exclusion Principle, these four electrons are distributed as follows: 2p_x^2, 2p_y^1, 2p_z^1 , where each orbital holds two electrons with opposite spins.

The Principle's Role in Atomic and Molecular Properties

Electron Configuration and Stability

The Pauli Exclusion Principle is fundamental in determining the electron configuration of atoms. It ensures that:

Electrons fill orbitals in a manner that avoids having more than two electrons in the same orbital with identical quantum numbers.
This principle helps explain the stability of the electron configuration and contributes to the overall energy of the atom.

Chemical Bonding and Structure

The Pauli Exclusion Principle also impacts chemical bonding and molecular structure:

In molecules, the principle ensures that molecular orbitals follow similar rules to atomic orbitals. No two electrons in a molecule can have the same set of quantum numbers, which affects how electrons are shared or transferred in chemical bonds.
It helps explain why elements form bonds and how bonding affects molecular geometry and properties.

Pauli Exclusion Principle and the Periodic Table

The Pauli Exclusion Principle is crucial for the structure of the periodic table:

It accounts for the arrangement of elements in the table based on their electron configurations.
The principle ensures that electrons fill orbitals in a specific order, leading to the periodic trends observed across periods and groups.

Periodic Trends

Atomic Size: As more electrons are added to an atom, they fill orbitals according to the Pauli Exclusion Principle. This filling pattern affects atomic size and other properties.
Ionization Energy: The principle influences how tightly electrons are held by the nucleus, affecting the amount of energy required to remove an electron from an atom.

Limitations and Extensions

While the Pauli Exclusion Principle is fundamental, its implications are extended in more complex scenarios:

Quantum Mechanics: The principle is a cornerstone of quantum mechanics, helping to explain phenomena beyond basic atomic structure, including fermionic behavior and degenerate matter in astrophysical contexts.
Relativistic Effects: In extremely high-energy environments, relativistic effects come into play, and the Pauli Exclusion Principle continues to be essential in understanding the behavior of particles like electrons in such conditions.

Physical Implications of the Pauli Exclusion Principle

The Pauli Exclusion Principle has a wide range of consequences in the physical world:

Matter Occupies Space: The Pauli Exclusion Principle explains why atoms do not collapse into a dense ball of matter. Since electrons in an atom cannot all occupy the lowest energy state due to this principle, they are forced into higher energy levels. This spreading of electrons across different shells prevents the atom from shrinking into a smaller, denser form. Without this principle, all electrons could occupy the lowest energy state, resulting in a much denser form of matter.
Stability of Matter: The stability of matter is due to the Pauli Exclusion Principle. In a solid, for example, the exclusion principle forces electrons to occupy different energy levels, creating the structure of solids. It ensures that objects have a finite size and don’t collapse under their own weight. It also explains the rigidity of matter, as electrons in different energy levels resist being squeezed together.
Degenerate Matter: In extreme environments like white dwarfs and neutron stars, the Pauli Exclusion Principle plays a crucial role in supporting these objects against gravitational collapse. In white dwarfs, the pressure resisting collapse is due to electron degeneracy pressure a consequence of the exclusion principle. In neutron stars, it's neutron degeneracy pressure that resists further collapse. Without this principle, such stellar remnants would collapse into black holes much more easily.
Periodic Table and Chemical Behavior: The principle is the reason for the unique chemical properties of elements. The configuration of electrons in various orbitals dictates how atoms interact and bond with each other. For example, elements with similar outer electron configurations (like those in the same group of the periodic table) behave similarly in chemical reactions.

Pauli Exclusion Principle in Quantum Mechanics

In the realm of quantum mechanics, the Pauli Exclusion Principle is a manifestation of the properties of fermions. Fermions are particles that obey the Pauli Exclusion Principle, meaning they must occupy unique quantum states in any system. In contrast, bosons (particles like photons, with integer spins) are not subject to this exclusion rule, allowing them to occupy the same quantum state, which explains phenomena like Bose-Einstein condensation.

Mathematically, the exclusion principle is built into the quantum mechanical description of fermions through antisymmetric wavefunctions. In quantum mechanics, the wavefunction of a multi-fermion system must change sign when two identical fermions are swapped. This antisymmetry enforces the exclusion principle because if two fermions were in the same state, swapping them would result in a wavefunction that equals zero, which is physically impossible.

Historical and Modern Significance

Wolfgang Pauli’s insight into the behavior of electrons earned him the Nobel Prize in Physics in 1945, recognizing the profound impact of the Pauli Exclusion Principle on atomic theory and quantum mechanics. Today, the principle remains one of the foundational laws of quantum physics and is critical in fields ranging from atomic physics to condensed matter physics, and even cosmology.

Chemistry FAQ

In multi-electron atoms, the Pauli Exclusion Principle states that no two electrons can have the same set of four quantum numbers: n (principal quantum number), l (azimuthal quantum number), m_l (magnetic quantum number), and m_s (spin quantum number). This explains the structure of the electron shells and the unique arrangement of electrons in orbitals.

For example, in a 2p subshell with three degenerate orbitals, each orbital can hold a maximum of two electrons, but they must have opposite spins (one with +1/2, and one with -1/2 ).
This principle also underlies the electron configuration in heavier elements and explains periodic trends, such as atomic size and ionization energy.

The Pauli Exclusion Principle plays a key role in the structure of white dwarfs and neutron stars through a concept known as degeneracy pressure.

In white dwarfs, electron degeneracy pressure arises because electrons are fermions and cannot occupy the same quantum state. This pressure prevents the star from collapsing under gravity once nuclear fusion ceases.
In neutron stars, the pressure comes from neutron degeneracy, where neutrons, which are also fermions, resist being squeezed into the same quantum state. The Pauli Exclusion Principle thus prevents further collapse, unless the star exceeds the Tolman-Oppenheimer-Volkoff limit, leading to the formation of a black hole.

The Pauli Exclusion Principle ensures that each electron in an atom or molecule has a unique set of quantum numbers. This results in the distinct arrangement of electrons in orbitals and explains the electronic structure that underpins the chemical properties of elements.

For example, the principle explains why only two electrons can occupy an s-orbital (with opposite spins) and why higher orbitals (p, d, f) accommodate more electrons by having more combinations of quantum numbers.
In molecular orbital theory, it helps explain the bonding and anti-bonding orbitals that determine the stability of molecules.

The Pauli Exclusion Principle is critical in the band theory of solids, which describes the behavior of electrons in metals, semiconductors, and insulators.

In solids, electrons occupy energy bands instead of discrete atomic orbitals. The Pauli Exclusion Principle restricts multiple electrons from occupying the same quantum state within these bands, leading to the formation of the valence band (filled with electrons) and the conduction band (where electrons can move freely, allowing electrical conductivity).
In metals, the conduction band overlaps with the valence band, while in semiconductors and insulators, the band gap between these bands influences conductivity, with the Pauli Exclusion Principle dictating how many electrons can occupy the available states.

While the Pauli Exclusion Principle is most commonly applied to electrons, it governs the behavior of all fermions, including neutrons, protons, and certain types of atoms (e.g., helium-3). Fermions are particles with half-integer spin, and the exclusion principle prevents any two fermions from sharing the same quantum state.

In nuclear physics, the principle dictates the arrangement of protons and neutrons within an atomic nucleus, influencing the stability and structure of isotopes.
In quantum gases, such as Fermi gases, the exclusion principle leads to the formation of Fermi levels and explains why fermions at absolute zero occupy a range of energy states rather than collapsing into a single state like bosons. This behavior has been observed in systems like ultracold atomic gases, leading to insights in quantum statistics.

Conclusion

The Pauli Exclusion Principle is a cornerstone of quantum mechanics, explaining the structure of atoms, the behavior of fermions, and the stability of matter. Its implications extend across physics, influencing how matter forms, why the periodic table is structured as it is, and why objects have volume and resist compression. Without the Pauli Exclusion Principle, the universe would be radically different, and the familiar structure of matter would not exist. Understanding this principle is key to unlocking the mysteries of both the micro and macro scales of the physical world.

Tags :